排序算法
ssk-wh Lv4
  2021-10-12 12:30:38 2021-10-12 12:30   2024-03-18 01:35:39  3.9k Words  17 Mins  

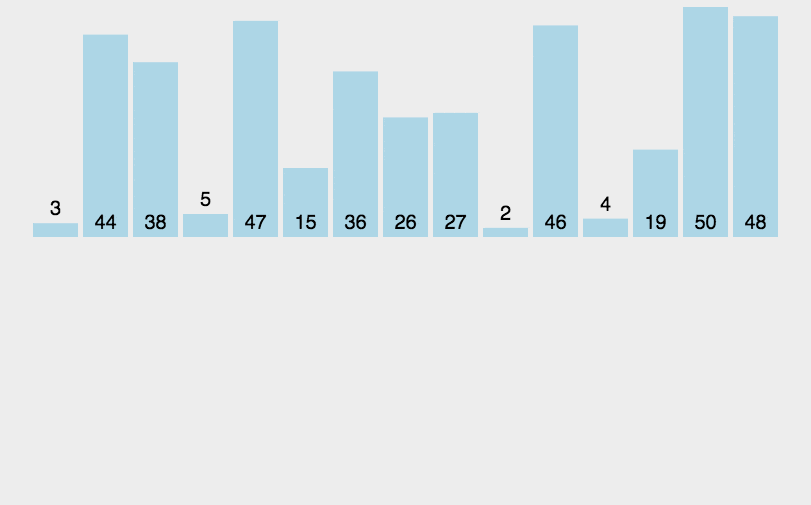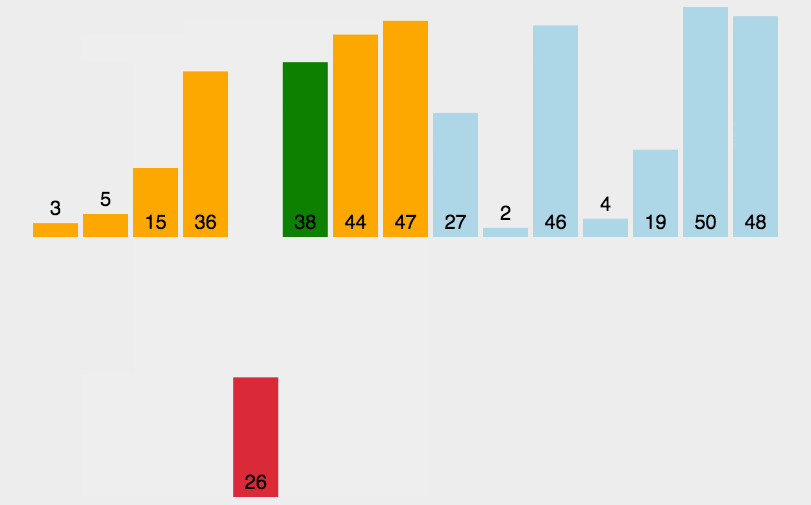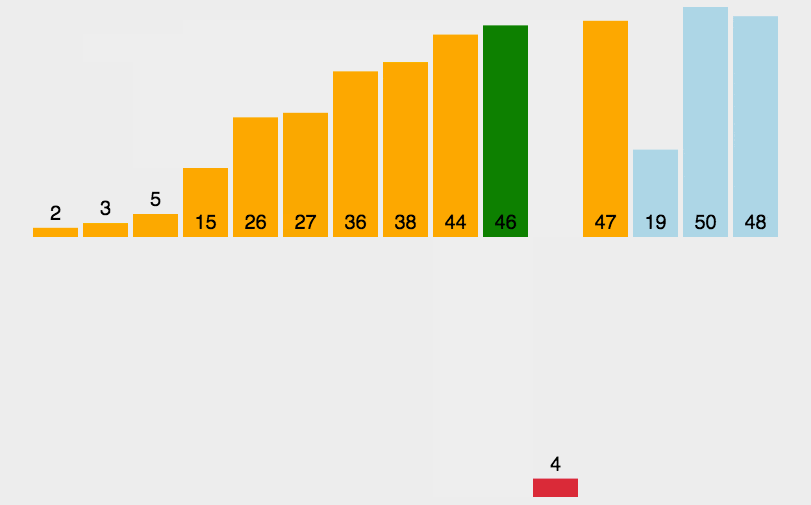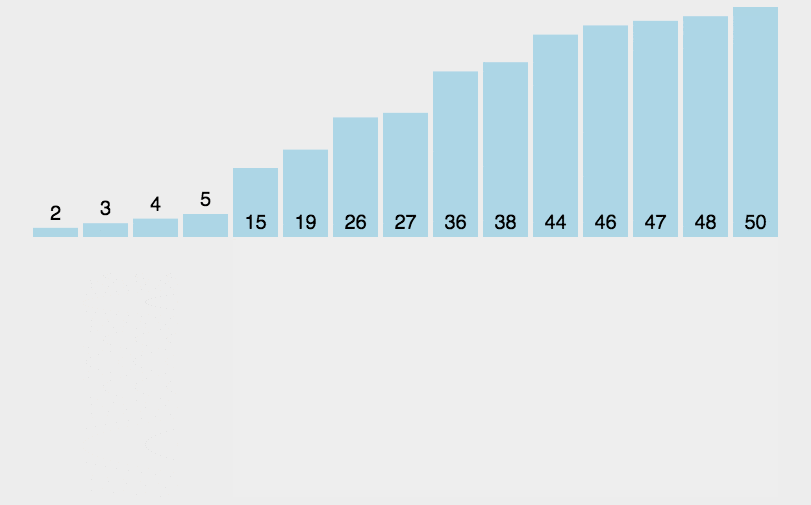
冒泡排序

重复地遍历待排序的数列，每次比较相邻的两个元素，如果顺序错误就交换它们，直到没有相邻元素需要交换为止。在每一轮遍历中，都会将待排序序列中的最大元素移到序列的末尾。

步骤

具体实现过程如下：

从待排序序列的第一个元素开始，依次比较相邻的两个元素，如果顺序错误就交换它们。

继续向下遍历，比较相邻的两个元素，并进行交换。

重复上述步骤，直到没有相邻元素需要交换为止。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <stdio.h>

void bubble_sort(int arr[], int n) {
    int i, j, temp;
    // 遍历整个数组 n - 1 次
    for (i = 0; i < n - 1; i++) {
        // 每次遍历将最大值放在数组末尾，因此只需要遍历 n - i - 1 次
        for (j = 0; j < n - i - 1; j++) {
            // 如果相邻的元素顺序错误，则交换它们的位置
            if (arr[j] > arr[j+1]) {
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
}

int main() {
    int arr[] = {5, 3, 8, 4, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    int i;
    printf("原数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    bubble_sort(arr, n);
    printf("排序后的数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return 0;
}

这个程序将数组 {5, 3, 8, 4, 2} 进行冒泡排序，并输出结果：

1
2
原数组为：5 3 8 4 2 
排序后的数组为：2 3 4 5 8

选择排序

它的基本思想是在待排序的序列中找到最小（或最大）的元素，将其放在序列的起始位置，然后再在剩余的元素中继续寻找最小（或最大）的元素，放在已排序的序列末尾。以此类推，直到所有元素都排序完成

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <stdio.h>

void selectionSort(int arr[], int len) {
    for (int i = 0; i < len - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        if (minIndex != i) {
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }
}

int main() {
    int arr[] = {3, 5, 1, 4, 2};
    int len = sizeof(arr) / sizeof(arr[0]);
    selectionSort(arr, len);
    for (int i = 0; i < len; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

插入排序

插入排序是一种简单的排序算法，它基于插入的思想。在插入排序中，将待排序的元素从未排序的序列中逐个取出，并将其插入到已排序的序列中的正确位置，直到所有元素都被插入到已排序的序列中为止。

步骤

具体来说，插入排序分为两个步骤：
（1）将待排序的第一个元素视为已排序的序列，然后将第二个元素插入到已排序的序列中的正确位置；
（2）重复执行上述步骤，直到所有元素都被插入到已排序的序列中。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <stdio.h>

void selection_sort(int arr[], int n) {
    int i, j, min_index, temp;
    // 遍历整个数组 n - 1 次
    for (i = 0; i < n - 1; i++) {
        min_index = i;
        // 在剩余未排序的元素中寻找最小值的下标
        for (j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }
        // 将最小值与已排序序列末尾元素交换位置
        temp = arr[min_index];
        arr[min_index] = arr[i];
        arr[i] = temp;
    }
}

int main() {
    int arr[] = {5, 3, 8, 4, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    int i;
    printf("原数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    selection_sort(arr, n);
    printf("排序后的数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return 0;
}

这个程序将数组 {5, 3, 8, 4, 2} 进行选择排序，并输出结果：

1
2
3
原数组为：5 3 8 4 2 
排序后的数组为：2 3 4 5 8

快速排序

基本思想是通过一趟排序将待排序的数据分割成独立的两部分，其中一部分的所有元素都比另外一部分的所有元素都小，然后分别对这两部分继续进行快速排序，直到整个序列有序。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>

int partition(int arr[], int low, int high) {
    int pivot = arr[low];  // 选取第一个元素作为基准值
    while (low < high) {
        while (low < high && arr[high] >= pivot) {
            high--;
        }
        arr[low] = arr[high];
        while (low < high && arr[low] <= pivot) {
            low++;
        }
        arr[high] = arr[low];
    }
    arr[low] = pivot;
    return low;
}

void quicksort(int arr[], int low, int high) {
    if (low < high) {
        int pivotPos = partition(arr, low, high);  // 将数组划分为两部分
        quicksort(arr, low, pivotPos - 1);  // 递归调用
        quicksort(arr, pivotPos + 1, high);
    }
}

int main() {
    int arr[] = {3, 5, 1, 4, 2};
    int len = sizeof(arr) / sizeof(arr[0]);
    quicksort(arr, 0, len - 1);
    for (int i = 0; i < len; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

归并排序

步骤

快速排序的具体实现过程如下：

从数列中挑出一个元素，称为基准（pivot）。
重新排序数列，将所有比基准值小的元素放在基准前面，所有比基准值大的元素放在基准的后面。在这个分割结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <stdio.h>

void quick_sort(int arr[], int left, int right) {
    int i = left, j = right, pivot = arr[(left + right) / 2], temp;
    // 分区操作
    while (i <= j) {
        while (arr[i] < pivot) {
            i++;
        }
        while (arr[j] > pivot) {
            j--;
        }
        if (i <= j) {
            temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++;
            j--;
        }
    }
    // 递归调用快速排序
    if (left < j) {
        quick_sort(arr, left, j);
    }
    if (i < right) {
        quick_sort(arr, i, right);
    }
}

int main() {
    int arr[] = {5, 3, 8, 4, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    int i;
    printf("原数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    quick_sort(arr, 0, n - 1);
    printf("排序后的数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return 0;
}

这个程序将数组 {5, 3, 8, 4, 2} 进行快速排序，并输出结果：

1
这个程序将数组 {5, 3, 8, 4, 2} 进行快速排序，并输出结果：

计数排序

计数排序是一种线性时间复杂度的排序算法，用于对整数序列进行排序。它的基本思想是统计每个元素出现的次数，然后按照元素的大小顺序将它们输出到结果数组中。

步骤

计数排序的实现步骤如下：

找出待排序的数组中最大和最小的元素。
统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项。
对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）。
反向填充目标数组：将每个元素 i 放在目标数组的第 C(i) 项，每放一个元素就将 C(i) 减去 1。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>
#include <stdlib.h>

void counting_sort(int arr[], int n) {
    // 找出最大和最小元素
    int max_num = arr[0], min_num = arr[0];
    for (int i=1; i<n; i++) {
        if (arr[i] > max_num) {
            max_num = arr[i];
        }
        if (arr[i] < min_num) {
            min_num = arr[i];
        }
    }

    // 统计元素出现次数
    int count_arr[max_num - min_num + 1];
    for (int i=0; i<=max_num-min_num; i++) {
        count_arr[i] = 0;
    }
    for (int i=0; i<n; i++) {
        count_arr[arr[i]-min_num]++;
    }

    // 对所有计数累加
    for (int i=1; i<=max_num-min_num; i++) {
        count_arr[i] += count_arr[i-1];
    }

    // 反向填充目标数组
    int sorted_arr[n];
    for (int i=n-1; i>=0; i--) {
        sorted_arr[count_arr[arr[i]-min_num]-1] = arr[i];
        count_arr[arr[i]-min_num]--;
    }

    // 将排序后的数组复制回原数组
    for (int i=0; i<n; i++) {
        arr[i] = sorted_arr[i];
    }
}

int main() {
    int arr[] = {10, 7, 3, 5, 8, 9, 1, 2, 4, 6};
    int n = sizeof(arr)/sizeof(int);
    
    counting_sort(arr, n);

    for (int i=0; i<n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
  
    return 0;
}

输出结果为：

1
输出结果为：1 2 3 4 5 6 7 8 9 10

希尔排序

希尔排序（Shell Sort）是一种基于插入排序的排序算法，它通过将原数组划分成多个子序列来改进插入排序，从而提高排序效率。希尔排序的基本思想是将相距某个“增量”的元素组成一个子序列进行插入排序，然后逐步缩小增量，直到增量为1，完成最后一次插入排序，最终达到整个序列有序的目的。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <stdio.h>
#include <stdlib.h>

void shell_sort(int arr[], int n) {
    int gap, i, j, temp;
    for (gap = n / 2; gap > 0; gap /= 2) {
        for (i = gap; i < n; i++) {
            temp = arr[i];
            for (j = i; j >= gap && arr[j-gap] > temp; j -= gap) {
                arr[j] = arr[j - gap];
            }
            arr[j] = temp;
        }
    }
}

int main() {
    int arr[] = {10, 7, 3, 5, 8, 9, 1, 2, 4, 6};
    int n = sizeof(arr)/sizeof(int);
    
    shell_sort(arr, n);

    for (int i=0; i<n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
  
    return 0;
}

输出结果为：

1
输出结果为：输出结果为：1 2 3 4 5 6 7 8 9 10

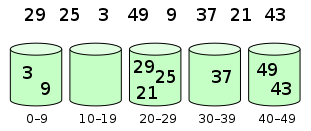
桶排序

桶排序（Bucket Sort）是一种基于计数排序的排序算法，它利用了映射函数将原数组中的元素映射到有限数量的桶（bucket）中，并在每个桶中分别进行排序，最终将所有桶中的元素合并成一个有序的数组。桶排序适用于待排序元素的范围比较小，且元素分布较为均匀的情况下，时间复杂度可以达到线性级别。

元素分布在桶中：

image

然后，元素在每个桶中排序：

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <stdio.h>

#define ARRAY_SIZE 10
#define BUCKET_SIZE 10

void bucket_sort(int arr[], int n) {
    int i, j;
    int bucket[BUCKET_SIZE] = {0};

    for (i = 0; i < n; ++i) {
        ++bucket[arr[i]];
    }

    for (i = 0, j = 0; j < BUCKET_SIZE; ++j) {
        while (bucket[j] > 0) {
            arr[i++] = j;
            --bucket[j];
        }
    }
}

int main() {
    int arr[ARRAY_SIZE] = {8, 4, 2, 5, 9, 1, 6, 3, 7, 0};
    int i;

    printf("Before sorting: ");
    for (i = 0; i < ARRAY_SIZE; ++i) {
        printf("%d ", arr[i]);
    }

    bucket_sort(arr, ARRAY_SIZE);

    printf("\nAfter sorting: ");
    for (i = 0; i < ARRAY_SIZE; ++i) {
        printf("%d ", arr[i]);
    }

    return 0;
}

输出结果为：

1
2
Before sorting: 8 4 2 5 9 1 6 3 7 0 
After sorting: 0 1 2 3 4 5 6 7 8 9

堆排序

堆排序（Heap Sort）是一种基于完全二叉树结构的排序算法，它利用堆这种数据结构来实现排序。堆可以看作是一种优先队列，它满足以下性质：

父节点的值大于或等于（小于或等于）其子节点的值，称为大根堆（小根堆）；
堆是一个完全二叉树，除了最后一层节点可能不满，其他层节点都是满的。
堆排序的基本思路是，首先将待排序数组构建成一个大根堆或小根堆，然后将堆顶元素与堆末元素交换，再重新调整堆结构，直到排序完成。

image
image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <stdio.h>

void heapify(int arr[], int root, int end) {
    int parent = root;
    int child = 2 * parent + 1; // 左子节点
    while (child <= end) {
        // 如果右子节点存在且值大于左子节点，则选择右子节点
        if (child + 1 <= end && arr[child] < arr[child + 1]) {
            child++;
        }
        // 如果父节点值大于等于子节点值，则退出循环
        if (arr[parent] >= arr[child]) {
            break;
        }
        // 否则交换父子节点的值，并继续向下调整
        int temp = arr[parent];
        arr[parent] = arr[child];
        arr[child] = temp;
        parent = child;
        child = 2 * parent + 1;
    }
}

void heap_sort(int arr[], int n) {
    // 将待排序数组构建为一个大根堆
    for (int i = (n - 1) / 2; i >= 0; i--) {
        heapify(arr, i, n - 1);
    }
    // 不断将堆顶元素与堆末元素交换，并重新调整堆结构，直到排序完成
    for (int i = n - 1; i > 0; i--) {
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
        heapify(arr, 0, i - 1); // 减小堆的大小
    }
}

int main() {
    int arr[] = {5, 3, 8, 4, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    int i;
    printf("原数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    heap_sort(arr, n);
    printf("排序后的数组为：");
    for (i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    return 0;
}

输出结果为：

1
2
3
原数组为：5 3 8 4 2 
排序后的数组为：2 3 4 5 8

基数排序

基数排序（Radix Sort）是一种非比较排序算法，它将待排序的元素拆分成若干个位数或字符，然后按照每个位数或字符分别进行排序。基数排序可以使用桶排序实现。

image

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>
#include <stdlib.h>

// 获取数组中最大值
int getMax(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; ++i)
        if (arr[i] > max)
            max = arr[i];
    return max;
}

// 对给定数字根据 exp 进行计数排序
void countSort(int arr[], int n, int exp) {
    int output[n]; // 存储 (arr 中元素根据 exp 计算出来的) 排序结果的辅助数组
    int i, buckets[10] = {0}; // 创建包含 10 个桶的数组，并初始化每个桶的数量为 0

    // 将数据分配到桶中
    for (i = 0; i < n; ++i)
        buckets[(arr[i] / exp) % 10]++;

    // 修改桶，使每个桶存储该桶前面所有桶中元素的数量总和
    for (i = 1; i < 10; ++i)
        buckets[i] += buckets[i - 1];

    // 根据 exp 和已分配到的桶，将数据存储到 output 数组中
    for (i = n - 1; i >= 0; --i) {
        output[buckets[(arr[i] / exp) % 10] - 1] = arr[i];
        buckets[(arr[i] / exp) % 10]--;
    }

    // 从 output 拷贝回 arr 数组，相当于更新原数组
    for (i = 0; i < n; ++i)
        arr[i] = output[i];
}

// 基数排序主函数
void radixSort(int arr[], int n) {
    int exp, max = getMax(arr, n);

    // 从个位数开始排到最高位，依次按照不同数位进行计数排序
    for (exp = 1; max / exp > 0; exp *= 10)
        countSort(arr, n, exp);
}

int main() {
    int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
    int n = sizeof(arr) / sizeof(arr[0]);

    radixSort(arr, n);

    printf("Sorted array: \n");
    for (int i = 0; i < n; ++i)
        printf("%d ", arr[i]);
    return 0;
}

输出结果为：

1
2
3
Sorted array: 
2 24 45 66 75 90 170 802

注意

在实现基数排序时，需要注意以下几点：

获取数组中最大元素的位数：可以使用一个函数来获取数组中最大元素的位数，例如 get_max_digit 函数。

创建桶：因为每个桶都是一个数组，所以可以使用一个指向指针数组的指针来表示桶数组，例如 int *buckets[10]。

将元素放入桶中：对于每个元素，根据其当前位数上的数值将其放入对应的桶中。

将桶中的元素按顺序放回数组中：按照从小到大的顺序依次将桶中的元素放回数组中，这里可以使用一个计数器来记录放回数组的元素的位置。

清空桶：在每次使用完桶之后，需要将桶中的元素清空，以便下一次使用。

当待排序元素为整数类型时，基数排序可以比快速排序、归并排序等算法更快地完成排序。

同时需要注意，基数排序的实现比较复杂，尤其是在涉及到整数位数的时候，需要花费较多的时间进行调试。

附

本文图片资源来自 菜鸟教程

 Comments
  1. 冒泡排序
  2. 选择排序
  3. 插入排序
  4. 快速排序
  5. 归并排序
  6. 计数排序
  7. 希尔排序
  8. 桶排序
  9. 堆排序
  10. 基数排序
  11. 附